三角関数やサイン・コサイン・タンジェントという用語を聞いてどのように感じますでしょうか。

筆者はもともと数学が苦手でこれまで避け続けてきましたが、color-mix() 関数の色相補間の方法を紹介する記事のデモを作成するために、CSS の sin()、cos() の 2 つの関数を使ったのをきっかけに、少しずつ興味を持ち、身近に感じられるようになりました。

この記事では、そのような数学に苦手意識のある人間の視点から、CSS に導入された sin()、cos()、tan() を試しながら三角関数の基礎を学習していきます。

三角関数の基礎

見出し「三角関数の基礎」

三角関数の大きな特徴として、直角三角形の角度 θ（シータ）と一辺の長さがわかっていれば、残りの辺の長さを計算できることが挙げられます。

数学がとっつきにくい理由のひとつが、この「θ（シータ）」のように日常生活ではあまり見かけない記号や公式が出現することにあります。インタラクティブなデモを操作したり自分でコードを書くことで、その仕組みへの理解が深まる（と思う）ので、もし抵抗を感じたとしても一旦そのまま進みましょう。

以下は、C の角度が 90° の直角三角形を描いたデモです。三角形は CSS の clip-path プロパティを使用して描画しており、スライダーを操作することで、A の角度（θ）が変わります。

Live Demo

このデモは、お使いのブラウザでは対応していません 🙇‍♂️

30 deg

clip-path プロパティで三角形を描くには、polygon() を使ってポイントの座標を指定するのが一般的です。そのため、A、B、C のそれぞれの座標を求める必要があります。

まず、A、C の座標はそれぞれ 0 100% と 100% 100% です。残った B の x 座標は 100% ですが、y 座標はどのように求めればよいでしょうか。

clip-path プロパティを使用して直角三角形を描画する
.triangle {
  inline-size: 200px;
  aspect-ratio: 1;
  background-color: #007373;
  clip-path: polygon(
    /* A */ 0 100%,
    /* B */ 100% var(--b-y), /* 📐 頂点　B の y 座標を求める */
    /* C */ 100% 100%
  );
}

ここで、直角三角形のそれぞれの辺の名称と、三角関数の定義を見てみましょう。

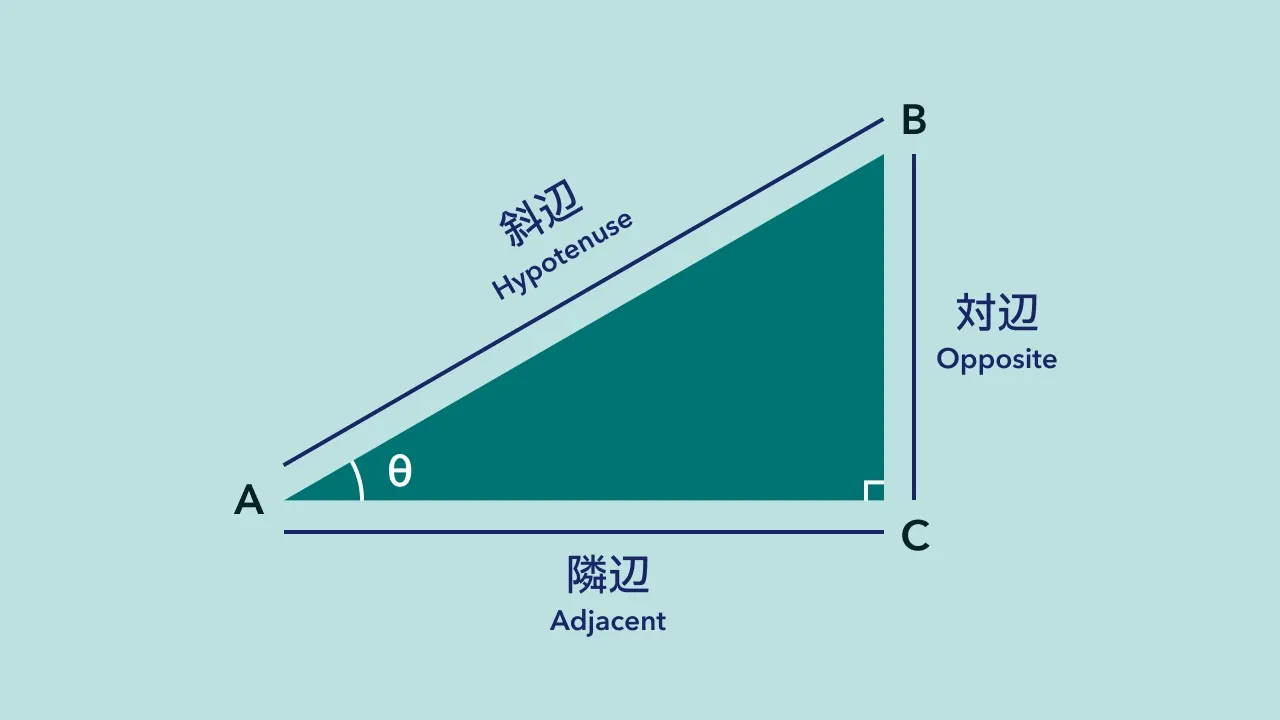
直角三角形の辺の名称を示した図。角 A から角 B は斜辺、角 B から角 C は対辺、角 A から角 C は隣辺と呼ばれる
直角三角形のそれぞれの辺の名称

これらの辺の名称は θ（シータ）を基準としています。

θ から斜めに伸びる辺は「斜辺（Hypotenuse）」、向かい側にある辺は「対辺（Opposite）」、隣接する辺は「隣辺（Adjacent）」と呼びます。

そして、これらの辺と三角関数は以下の定義が成り立ちます。

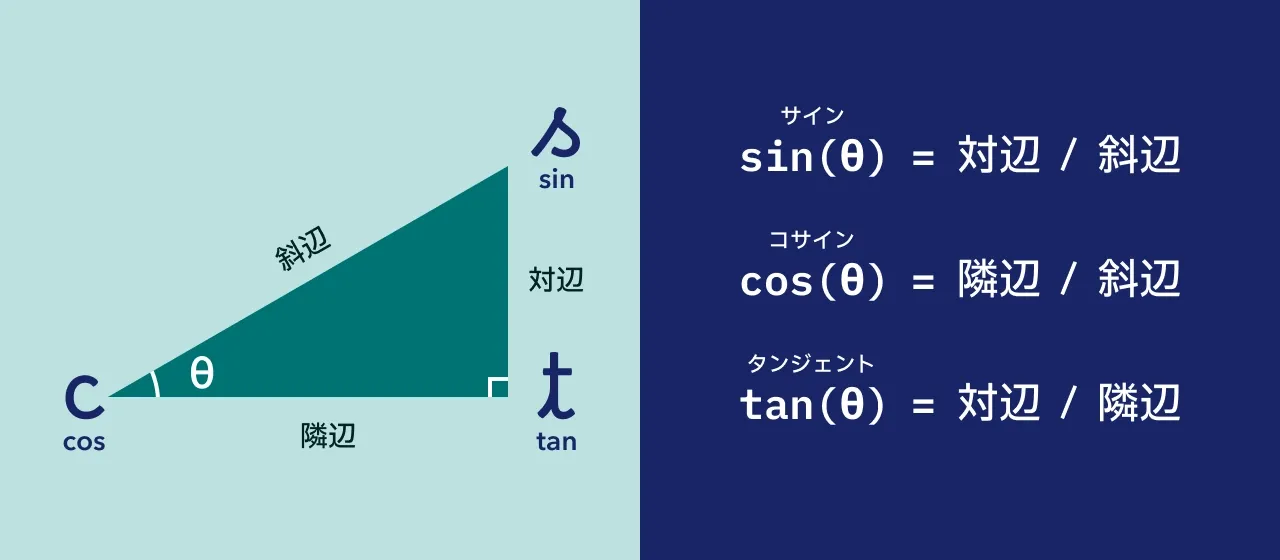
sin(θ) = 対辺 / 斜辺。cos(θ) = 隣辺 / 斜辺。tan(θ) = 対辺 / 隣辺
直角三角形による三角関数の定義1

ここまでの内容がなんとなく理解できたら、再びデモを確認します。

Live Demo

このデモは、お使いのブラウザでは対応していません 🙇‍♂️

30 deg

頂点 B の y 座標は、直角三角形の対辺の一番上に位置することがわかります。

現時点では角度（θ）と隣辺のサイズがわかっている状態なので、tan(θ) の等式を変形すると対辺の長さを求めることができます。

tan(θ) = 対辺 / 隣辺
対辺 = tan(θ) * 隣辺

この式から求めた対辺の長さを全体の高さから引いた値が、頂点 B の y 座標です。

tan() 関数を使用した例
.triangle {
  /* 角度（θ） */
  --angle: 30;

  /* 対辺 = tan(θ) * 隣辺 */
  --opposite: calc(tan(var(--angle) * 1deg) * 100%);

  /* 頂点 B の y 座標 = 全体の高さ - 対辺 */
  --b-y: calc(100% - var(--opposite));
}

この CSS 変数を、最初のコードに反映して完成です。--angle は HTML の style 属性に移動させました。値を変更して直角三角形の変化を確認してみてください。

clip-path プロパティを使用して三角形を描画する例
<!-- HTML -->
<div class="triangle" style="--angle: 30;"></div>

<!-- CSS -->
<style>
.triangle {
  /* 対辺 = tan(θ) * 隣辺 */
  --opposite: calc(tan(var(--angle) * 1deg) * 100%);

  /* 頂点 B の y 座標 = 全体の高さ - 対辺 */
  --b-y: calc(100% - var(--opposite));

  inline-size: 200px;
  aspect-ratio: 1;
  background-color: #007373;
  clip-path: polygon(
    0 100%,
    100% var(--b-y),
    100% 100%
  );
}
</style>

このように三角関数は、直角三角形の角度（θ）と一辺の長さから、残りの辺の長さを求めたいときに役立つ関数であることがわかります。

三角関数は古来よりさまざまな場面で活用され、星を見上げる角度から暦をつくるときや、測量によって地図を作成するときなど、人々の生活に欠かせないものでした。

現代においても、ゲームプログラミングや GPS をはじめ、画像圧縮や音声認識など、多種多様な技術に応用されており、実はとても身近な存在なのです。

sin()、cos()、tan() に指定できる数値

この見出しのリンク

JS の三角関数である Math.sin()、Math.cos()、Math.tan() で指定する引数の数値は、ラジアン（弧度法）2に限定されます。

CSS でも、例えば sin(1) のように、単位を付けずに数値のみを指定するとラジアンとして解釈されますが、deg で角度を指定したり（度数法）、turn で回転数を指定することもできます。

CSS の三角関数で指定できる数値の例
sin(90deg)          /* 角度（度数法） */
sin(1.5708rad)      /* ラジアン（弧度法） */
sin(1.5708)         /* 単位を指定しなければラジアンだと解釈される */
sin(pi / 2 * 1rad)  /* 定数 pi（円周率）と rad（ラジアン）の組み合わせ */
sin(0.25turn)       /* 回転数 */
sin(100grad)        /* グラード */

このように複数の選択肢がありますが、特別な理由がない場合には、多くの人にとって理解しやすい deg を使用するのがよいでしょう。

円周に沿って回転

見出し「円周に沿って回転」

続いて、三角関数を円に応用する例を見ていきます。

以下はスライダーを操作すると、オブジェクトが円周に沿って回転するデモです。このスタイルを実現するにはどのように指定すればよいでしょうか。

Live Demo

このデモは、お使いのブラウザでは対応していません 🙇‍♂️

0 deg

以下の図のように、中心点から回転する点 P までを結ぶと直角三角形を描くことができます。この直角三角形に対して三角関数を使うことで、点 P の座標がわかります。

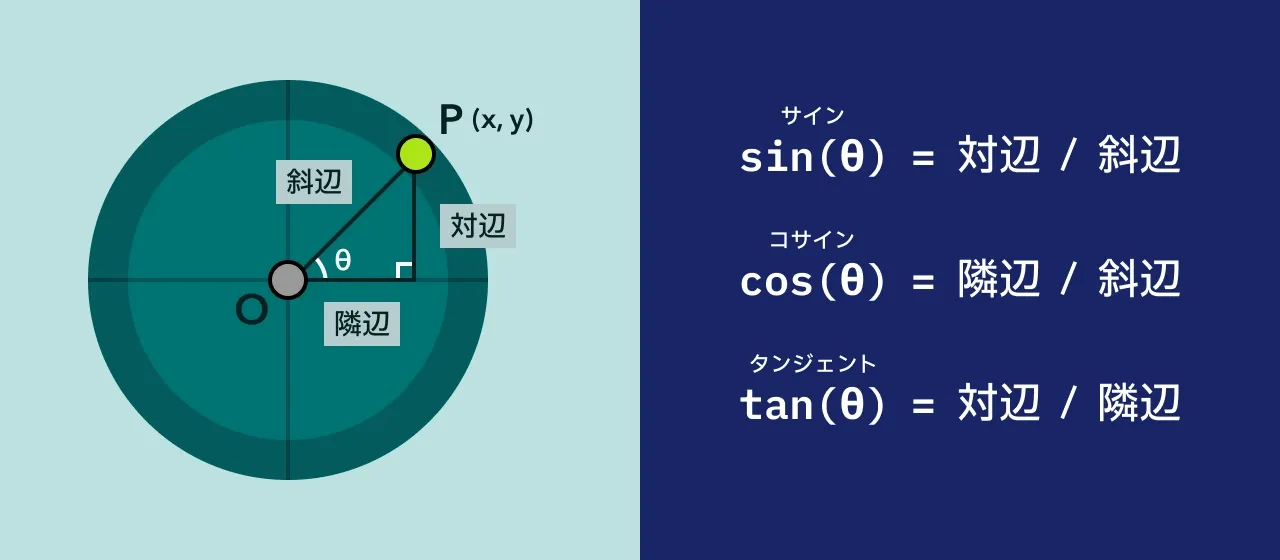
sin(θ) = 対辺 / 斜辺。cos(θ) = 隣辺 / 斜辺。tan(θ) = 対辺 / 隣辺
円のなかに現れた直角三角形に三角関数の定義を適用する

角度（θ）はスライダーで入力した値で、斜辺は円の半径です。水平方向に伸びる x 座標は隣辺で、垂直方向に伸びる y 座標は対辺です。

現時点では角度（θ）と斜辺のサイズがわかっている状態なので、三角関数を使用して、残りの x 座標（隣辺）と y 座標（対辺）を求めることができます。

x 座標の位置を求める式
cos(θ) = 隣辺 / 斜辺
隣辺 = cos(θ) * 斜辺
x 座標 = cos(θ) * 半径
y 座標の位置を求める式
sin(θ) = 対辺 / 斜辺
対辺 = sin(θ) * 斜辺
y 座標 = sin(θ) * 半径

これで、点 P の座標を求める式がわかったので、CSS に反映していきます。

まず、点 P に position: absolute を指定して円の中心に配置し、そこから translate プロパティを使用して x 座標、y 座標の位置に移動させて完成です。

HTML の style 属性で指定している --angle の値を変更して、円周の周りをオブジェクトが回転する変化を確認してみてください。

点 P を円周に配置する例
<!-- HTML -->
<div class="circle" style="--angle: 30;">
  <div class="circle-point"></div>
</div>

<!-- CSS -->
<style>
/* 円 */
.circle {
  /* 円の半径 */
  --circle-radius: 100px;

  /* 点 P の半径 */
  --point-radius: 10px;

  /* 斜辺: 円の半径から点 P の半径を引く */
  --radius: calc(var(--circle-radius) - var(--point-radius));

  position: relative;
  inline-size: calc(var(--circle-radius) * 2);
  aspect-ratio: 1;
  border-radius: 50%;
  background-color: hsl(180 100% 23%);
}

/* 点 P */
.circle-point {
  /* 円の中心に配置 */
  position: absolute;
  inset-block-start: calc(50% - var(--point-radius));
  inset-inline-start: calc(50% - var(--point-radius));

  /* 円周に移動 */
  translate:
    calc(cos(var(--angle) * 1deg) * var(--radius))
    calc(sin(var(--angle) * 1deg) * var(--radius) * -1);

  inline-size: calc(var(--point-radius) * 2);
  aspect-ratio: 1;
  border: solid 2px black;
  border-radius: 50%;
  background-color: hsl(77 80% 50%);
}
</style>

ちなみに、translate プロパティの Y 座標は、正の値では下方向に移動し、負の値では上方向に移動しますが、今回は反時計回りに移動させたかったので -1 を乗算しています。

/* 反時計回り */
.circle-point {
  translate:
    calc(cos(var(--angle) * 1deg) * var(--radius))
    calc(sin(var(--angle) * 1deg) * var(--radius) * -1);
}

/* 時計回り */
.circle-point {
  translate:
    calc(cos(var(--angle) * 1deg) * var(--radius))
    calc(sin(var(--angle) * 1deg) * var(--radius));
}

先ほどのデモに対して、円のなかに現れる直角三角形と、cos(θ)、sin(θ) のそれぞれの値の変化を可視化すると以下のようになります。

Live Demo

このデモは、お使いのブラウザでは対応していません 🙇‍♂️

0 deg
0
0

下部に表示されている、cos(θ) と sin(θ) の値3に注目すると、-1 から 1 の値を往来しているのがわかります。

角度を変更したときの cos(θ) と sin(θ) の動きは、後ほど説明する正弦波にも関わるので頭の片隅に置いておいてください。

ここまでに説明した仕組みを応用することで、CSS を使って円周に沿ってオブジェクトを配置することができます。以下はアナログ時計のデモです。

Live Demo

このデモは、お使いのブラウザでは対応していません 🙇‍♂️

200

時計の針は中心から rotate プロパティで回転させると実現できるので、三角関数は使用していませんが、円周に沿って配置された数字（インデックス）や目盛りには cos() と sin() を使用しています。

「clock size」のスライダーを操作すると時計のサイズが変化しますが、拡大してもそれらの要素の位置が維持されることがわかります。

また、「counter-style」のセレクトメニューの値を変更すると数字（インデックス）の表示が変わる機能も付けましたが、この見た目の変化は CSS の <counter-style> 4で実現しています。

以下は、円周に配置された数字（インデックス）のコードの抜粋です。

円周に沿って配置された数字（インデックス）の例
<!-- HTML -->
<div class="clock" style="--counter-style: decimal;">
  <div>
    <!-- 数字（インデックス）の数だけ要素を用意 -->
    <span class="clock-index"></span>
    <span class="clock-index"></span>
    <span class="clock-index"></span>
    <span class="clock-index"></span>
    <span class="clock-index"></span>
    <span class="clock-index"></span>
    <span class="clock-index"></span>
    <span class="clock-index"></span>
    <span class="clock-index"></span>
    <span class="clock-index"></span>
    <span class="clock-index"></span>
    <span class="clock-index"></span>
  </div>
</div>

<!-- CSS -->
<style>
.clock {
  position: relative;
  container-type: size;
  inline-size: 200px;
  aspect-ratio: 1;
  border-radius: 50%;
  box-shadow: 0 0 0 4px inset hsl(180 94% 19%);
  background-color: hsl(180 100% 23%);
}
.clock-index {
  /* 角度の初期値 */
  --angle: 0;

  /* 時計の周囲の余白 */
  --gutter: 16px;

  /* 位置調整用の余白 */
  --padding: 0.2em;

  /* 半径 */
  --radius: calc(50cqi - (var(--gutter) / 2));

  position: absolute;
  inset-block-start: calc(50% - 1em);
  inset-inline-start: calc(50% - 1em);
  inline-size: 2em;
  block-size: 2em;
  padding-block-start: var(--padding);
  counter-increment: hours;
  color: white;
  font-size: max(calc(1rem * 14 / 16), 5cqi);
  font-family: sans-serif;
  text-align: center;

  /* 円周に移動 */
  translate:
    calc(cos(var(--angle) * 1deg - 60deg) * (var(--radius) - var(--gutter) - var(--padding)))
    calc(sin(var(--angle) * 1deg - 60deg) * (var(--radius) - var(--gutter) - var(--padding)));
}
/* 数字は content プロパティに <counter-style> を指定して表現 */
.clock-index::after {
  content: counter(hours, var(--counter-style, decimal));
}
/* 数字（インデックス）の角度を指定 */
.clock-index:nth-child(2)  { --angle:  30; }
.clock-index:nth-child(3)  { --angle:  60; }
.clock-index:nth-child(4)  { --angle:  90; }
.clock-index:nth-child(5)  { --angle: 120; }
.clock-index:nth-child(6)  { --angle: 150; }
.clock-index:nth-child(7)  { --angle: 180; }
.clock-index:nth-child(8)  { --angle: 210; }
.clock-index:nth-child(9)  { --angle: 240; }
.clock-index:nth-child(10) { --angle: 270; }
.clock-index:nth-child(11) { --angle: 300; }
.clock-index:nth-child(12) { --angle: 330; }
</style>

円周に沿って配置する要素が多い場合には、このようにコード量が増えてしまうのが難点です。

SVG であれば、目盛と数字（インデックス）をコンパクトに 1 つにまとめることもできますが、CSS では見た目を柔軟に調整できるといった利点もあるので、目的やデザインにあわせて適切な方法を選択するのがよいでしょう。

正弦波

見出し「正弦波」

最後に三角関数と波の関係を見ていきます。

先ほどの円周に沿って回転するデモでは、角度を変更すると、sin(θ) と cos(θ) の値が -1 から 1 の間で変化していました。

以下は、sin(θ) と cos(θ) の値の変化に合わせて上下に移動するデモです。

「angle」のスライダーの値を変更したり、「PLAY」ボタンを選択して自動アニメーションを有効にして、その変化を確認してみてください。

Live Demo

このデモは、お使いのブラウザでは対応していません 🙇‍♂️

0 deg
0
0

0° と 360° の値は同じなので、前後につなげていくと周期的な変化になります。

この上下の変化を y 軸に配置し、x 軸を時間の経過とすると正弦波（サイン波）と呼ばれる波が描けます。波の高さ（振幅）は円の半径の長さと相関関係があります。

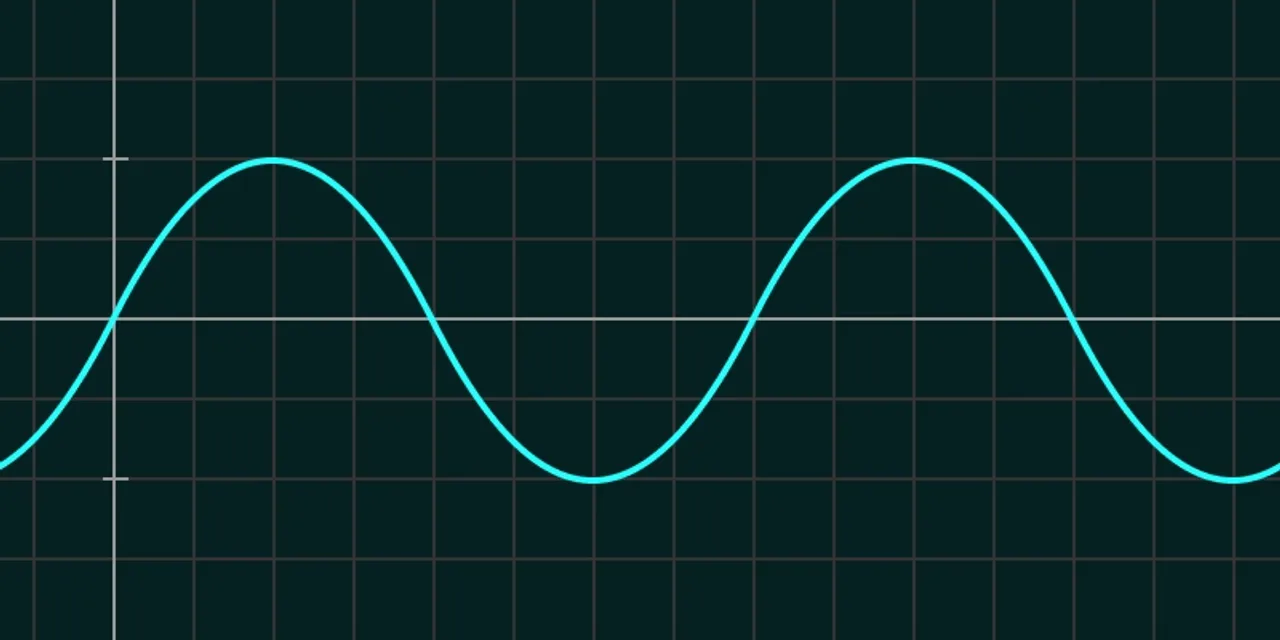
sin(θ) の値の変化を y 軸、時間の経過を x 軸として描いた正弦波のイラスト
正弦波（サイン波）

以下は、sin(θ) の波形に沿って要素を配置した例です。

Live Demo

このデモは、お使いのブラウザでは対応していません 🙇‍♂️

sin 0°

sin 30°

sin 60°

sin 90°

sin 120°

sin 150°

sin 180°

sin 210°

sin 240°

sin 270°

sin 300°

sin 330°

sin 360°

該当するコードを抜粋します。

sin(θ) の波形に沿って要素を配置した例
<!-- HTML -->
<div class="wave" style="--amplitude: 10em;">
  <p class="wave-item" style="--index: 0;">sin 0°</p>
  <p class="wave-item" style="--index: 1;">sin 30°</p>
  <p class="wave-item" style="--index: 2;">sin 60°</p>
  <p class="wave-item" style="--index: 3;">sin 90°</p>
  <p class="wave-item" style="--index: 4;">sin 120°</p>
  <p class="wave-item" style="--index: 5;">sin 150°</p>
  <p class="wave-item" style="--index: 6;">sin 180°</p>
  <p class="wave-item" style="--index: 7;">sin 210°</p>
  <p class="wave-item" style="--index: 8;">sin 240°</p>
  <p class="wave-item" style="--index: 9;">sin 270°</p>
  <p class="wave-item" style="--index: 10;">sin 300°</p>
  <p class="wave-item" style="--index: 11;">sin 330°</p>
  <p class="wave-item" style="--index: 12;">sin 360°</p>
</div>

<!-- CSS -->
<style>
.wave {
  display: flex;
  gap: 24px;
  place-items: center;
  overflow-x: auto;
  padding-block: calc(var(--amplitude, 10em) + 5em);
}
.wave-item {
  /* 要素の数 */
  --len: 13;

  /* 要素のサイズ */
  --item-size: 8em;

  /* インデックス番号から角度を算出 */
  --angle: calc(360deg / (var(--len) - 1) * var(--index));

  /* y 座標 */
  --translateY: calc(sin(var(--angle)) * var(--amplitude) * -1);

  display: grid;
  flex-shrink: 0;
  place-items: center;
  inline-size: var(--item-size);
  block-size: var(--item-size);
  padding: 1em;
  border: solid 4px hsl(180 94% 19%);
  border-radius: 50%;
  background-color: hsl(180 100% 23%);
  color: white;
  font-family: sans-serif;
  translate: 0 var(--translateY);
}
</style>

HTML の style 属性で指定している --amplitude は波形の振幅です。値を変更すると波の高さが変わります。

--angle は、360deg を要素数で割った角度にインデックス番号を乗算して、要素ごとの角度を算出しています。

.wave-item {
  /* インデックス番号から角度を算出 */
  --angle: calc(360deg / (var(--len) - 1) * var(--index));
}

y 座標は対辺なので、円周に沿って回転で説明した y 座標 = sin(θ) * 半径 の式を使います。

.wave-item {
  /* y 座標 */
  --translateY: calc(sin(var(--angle)) * var(--amplitude) * -1);
}

ちなみに、sin(θ) の代わりに cos(θ) を使うこともできますが、開始位置が異なるだけで波の形は sin(θ) と同じです。

Live Demo

このデモは、お使いのブラウザでは対応していません 🙇‍♂️

cos 0°

cos 30°

cos 60°

cos 90°

cos 120°

cos 150°

cos 180°

cos 210°

cos 240°

cos 270°

cos 300°

cos 330°

cos 360°

なお、CSS は曲線自体の描画には向いていません。ベジェ曲線のようになめらかに描画しようとすると、それだけ多くのポイントを配置する必要があるためです。

波形を曲線として描く場合には、<canvas> や SVG を使用するのがよいでしょう。

おわりに

見出し「おわりに」

この記事では、CSS に導入された sin()、cos()、tan() を使いながら、三角関数の説明を試みました。

これまで苦手意識のあった三角関数ですが、手を動かしながら仕組みを調べていくと興味が深まり身近に感じることができました。そして、学習のモチベーションには、その対象が社会や生活とつながっていると自覚することが大切であると再認識しました。

今回は調査しきれませんでしたが、そのほかの三角関数である asin()、acos()、atan()、atan2() に加え、pow() や sqrt() といった指数関数も CSS で使えるようになってきているので5、それらも含めて実用的な使い方を模索していければと考えています。

参考文献

見出し「参考文献」

本記事の作成にあたり、以下のウェブページや書籍を参考にしました。

脚注

  1. 日本では sin、cos、tan の頭文字「s」「c」「t」を筆記体で書いた順番（「分母 → 分子」の順）で関連する辺の位置を教えることが多いですが、英語圏では sin、cos、tan の頭文字と、辺の名称 ajacent、opposite、hypotenuse の頭文字を組み合わせて「SOHCAHTOA」と語呂合わせのように覚えるようです。また、英語では分数を読む順番が「分子 → 分母」のように日本と逆の順になりますが、演算するときにはこちらのほうが自然ではあります。 ↩

  2. ラジアン（弧度法）の説明は割愛しますが、詳しくは「ラジアン | Wikipedia」などをご参照ください。 ↩

  3. cos(θ) と sin(θ) の値は、小数点第 4 位までを表示しています。 ↩

  4. CSS Counter Styles Level 3 | W3C ↩

  5. The New CSS Math: pow(), sqrt(), and exponential friends | Dan Wilson ↩